Scendiamo nell’analisi della finale di Champions League NBL 2024 che ha regalato il quinto successo per Giancarlo Stagnitta, in una partita all’apparenza dominata, nonostante le ripetute chiamate effettuate da Simone Stagnitta.
Ci affidiamo alle statistiche NBLstats+ che scardinano e vanno oltre quello che possiamo vedere per offrirci una visione più dinamica e oggettiva della partita.
Partita segnata dalle aste, che però hanno solamente limato il punteggio finale e hanno permesso a Simone di arrivare secondo anziché terzo.
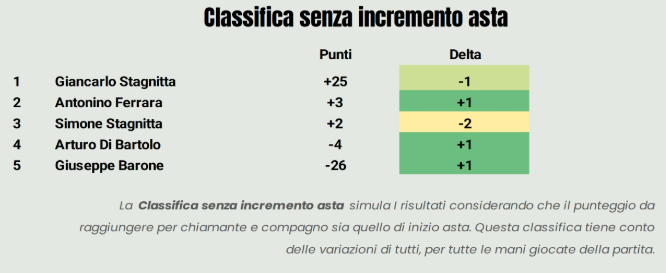
Per quanto riguarda il capitolo chiamate, da notare che le chiamate potenziali per Simone siano state ben 8, effettuandone 7. Erano 6 quelle potenziali per Giancarlo, effettuate 4. Non ci sono state sorprese per quanto riguarda le aste “rubate”, con il differenziale a zero per tutti i giocatori.
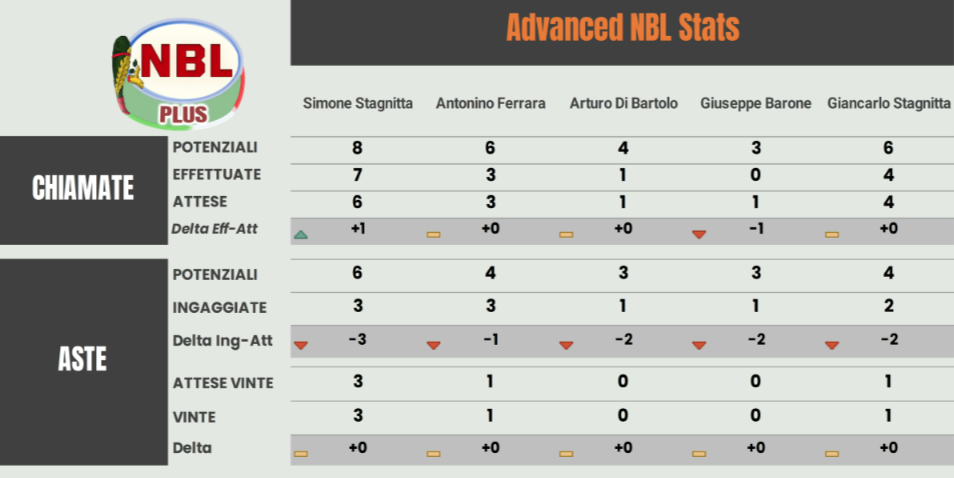
Passiamo all’analisi dei punteggi attesi, iniziando da quelli primari. Gli Xp primari ci forniscono una chiara visione sulla qualità delle carte ricevute: analizzano la mano su base statistica, si muovo anche simulando un giro al buio medio, sempre a livello statistico, pertanto forniscono un valore potenziale del punteggio base. Mettiamo gli Xp primari in parallelo con le probabilità di vittoria, che completano questa analisi fornendo quindi dei pronostici statistici, puramente in base alle carte ricevute.
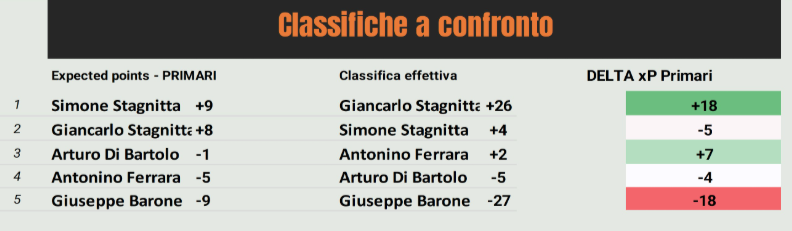
Estrema parità tra Giancarlo e Simone sulla carte per quanto concerne gli Xp primari e questo dato è confermato dalle probabilità di vittoria. Il grafico sotto indica la probabilità di avere un certo punteggio finale e si nota come i destini di Giancarlo e Simone sulla carta siano stati pressoché identici, con un leggero vantaggio per Simone.
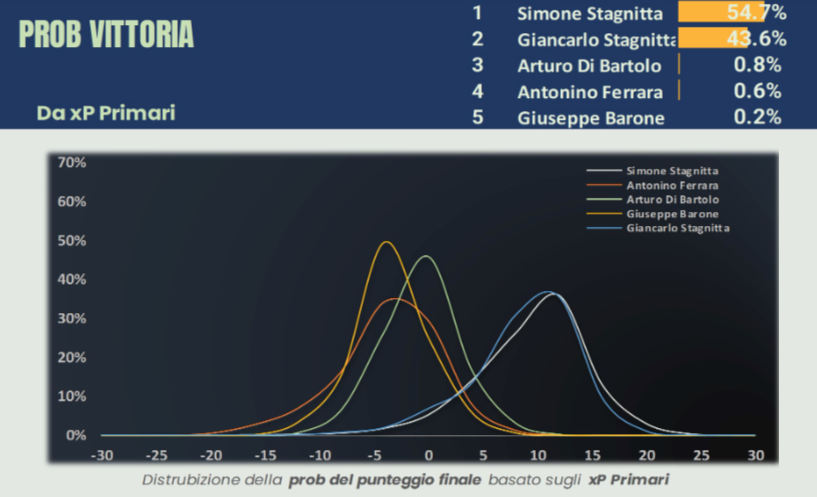
La partita però ha portato il risultato su binari completamente diversi ed è sufficiente introdurre gli Xp secondari per rendersi conto che la differenza abissale si è create nei giri al buio.

Il punteggio di Giancarlo è schizzato a +19 assoluti, mentre quello di Simone resta molto simile a quello primario. I Delta sono ora molto più contenuti, segno che la partita si sia mossa su binari standard. Il picco per Giancarlo si è spostato notevolmente in avanti e analizzando i grafici puntuali mano per mano, tornando agli Xp Primari, è facile capire dove Giancarlo abbia fatto la differenza.
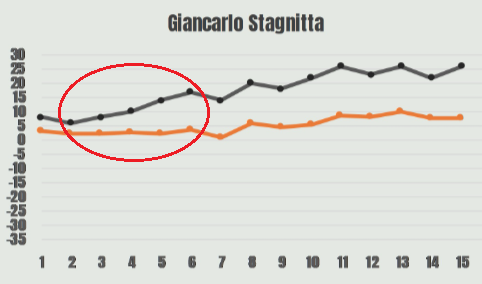
Tra la terza e la sesta mano riesce a costruire un gap positivo rispetto alle attese di circa 10 punti; la linea arancione rappresenta il punteggio atteso, mentre la linea nera è il punteggio reale della partita.
Alla terza mano incide anche una chiamata non effettuata da Giuseppe Barone; essa incide in maniera positiva per Giancarlo sopratutto nel confronto con Simone in quanto in questa chiamata Simone pesca proprio Giancarlo come compagno. In maniera assoluta invece, tornando al grafico, il differenziale è da vedere nei confronti della potenziale chiamata di Giuseppe, che non è stata effettuata, ma che in base alle condizioni del compagno (Nino Ferrara) avrebbe avuto solo il 44% di successo.
Alla mano 4 vince una mano da compagno con Arturo chiamante, in una mano con il 65% di probabilità di vittoria primaria, che viene “aggiustata” nel giro al buio dalla presa del chiamante stesso con una briscola bassa; decisiva in questo caso la posizione a chiudere del chiamante, che così facendo porta le probabilità al 77%.
La mano 5 merita un approfondimento separato perché risulta il punto di svolta dell’intera partita, forse l’unico appiglio per Simone. Richiede uno sforzo di apprendimento e strumenti non a porta di tutti; pertanto chi si sente soddisfatto dell’analisi condotta fino a qui può concludere la lettura.
Questa mano risulta clamorosamente un punto di non ritorno. La mano è stata chiamata da Simone, che insieme a Giuseppe, subisce un controcappotto. Se Simone avesse vinto questo mano, lasciando tutto il resto uguale, va detto che avrebbe comunque visto Giancarlo davanti, ma di pochissimi punti.
Tornando al campo la mano vede un giro al buio molto alto, con 111 punti (conteggio NBL) che porta la chiamata da una Xp primaria del 70% al 45%; inoltre l’asta, da 81 a 86 abbassa ancora di più la probabilità al 33%. Situazione quindi compromessa già in partenza.
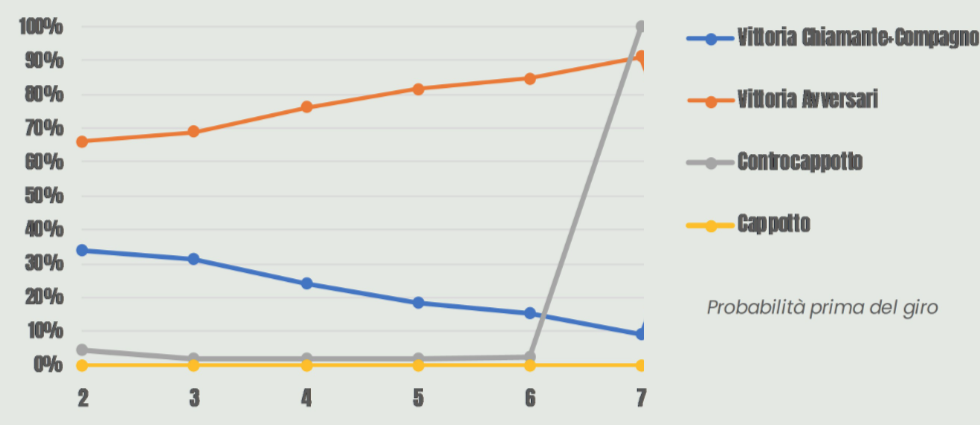
Giro dopo giro le probabilità di vittoria si abbassano fino a quando non arriva il giro 6. Prima di questo giro che parte da Giuseppe (compagno), la situazione vede i due con un giro scoperto da briscole ed è rimasta solo una briscola in mano agli avversari che è il 4 di coppe.
Simone vede quindi uno spiraglio, quando Giuseppe gioca il re di mazze. In quel momento, col 3 di mazze già giocato, restava solo l’asso di mazze, capace di prendere la mano, in assenza di briscole.
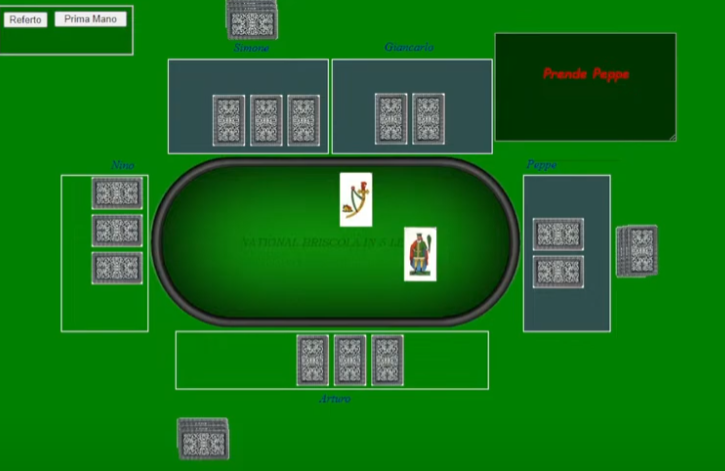
Dal punto di vista statistico, prima di questo giro la probabilità di vittoria era del 9%.
Introduciamo ora un’analisi strategica inedita che sfrutta i principi base della teoria dei giochi per selezionare la migliore strategia in modo analitico.
Per fare ciò, definiamo le condizioni iniziali e poniamo l’osservatore dal punto di vista di Simone. Passiamo così da un calcolo puramente statistico, utilizzato fino a oggi, a uno più puntuale e matematico, basato sullo stato dell’arte. Questo approccio considera sia le carte in mano a Simone sia lo stato del gioco in senso logico.
Simone ha in mano due briscole di coppe, che con certezza gli consentono di vincere due giri su tre, e un liscio che lascia un giro scoperto (Giuseppe non ha più briscole). Inoltre, tra le carte non ancora giocate ci sono il 4 di coppe e altri due assi, di cui uno è l’asso di mazze. Sapendo che il 3 di mazze è già stato giocato, Simone vede un’opportunità per tentare una giocata rischiosa. In questa sede analizziamo matematicamente se questa strategia abbia un fondamento logico e se possa portare a risultati favorevoli.
Gli scenari possibili sono due:
- Simone gioca il liscio.
- Simone decide di prendere il giro con una briscola e giocarsi la mano successiva.
Nel secondo scenario, la sconfitta della mano è certa al 100% quindi probabilità di vittoria pari al 0%, anche se consente di evitare un controcappotto. Questo dato non è a conoscenza di Simone il quale però ha la ragionevole certezza che possa verificarsi.
Col primo scenario, invece, si aprono tre sottoscenari distinti:
- Primo sottoscenario: Né Nino né Arturo possiedono l’asso di mazze o il 4 di coppe. In questo caso, Simone vince la mano. La probabilità di questo evento è del 13,3%.
- Secondo sottoscenario: Gli avversari vincono il giro, o con una briscola o di mano grazie all’asso di mazze. Questo evento, escludendo il rischio di controcappotto, ha una probabilità del 79,2%.
- Terzo sottoscenario: Si verifica il controcappotto. Ciò accade solo se Nino e Arturo possiedono sepratatamente l’asso di mazze e l’altro carico rimasto. La probabilità di questo evento è pari al 7,5%.
Riassumiamo quindi la situazione con questa simpatica tabella.
| Scenario | Descrizione | Probabilità che l’evento si verifichi |
|---|---|---|
| Scenario 1: Lascia il giro con il liscio | Simone gioca il liscio e non prende il giro. | |
| – Sottoscenario 1.1: Nessun asso di mazze né 4 di coppe | Né Nino né Arturo possiedono l’asso di mazze o il 4 di coppe, Simone vince la mano. | 13,3% |
| – Sottoscenario 1.2: Avversari vincono con briscola o asso di mazze | Gli avversari prendono il giro, o con briscola o con l’asso di mazze, senza effettuare controcappotto. | 79,2% |
| –Sottoscenario 1.3: avversari effettuano controcappotto | Si verifica il controcappotto, con Nino e Arturo che possiedono l’asso di mazze e un carico. | 7,5% |
| Scenario 2: Prende il giro con briscola | Simone prende il giro e si gioca la mano successiva. La sconfitta è certa. | 100% |
Occorre adesso fare un inciso importante per ciò che vogliamo introdurre. La probabilità di vittoria dell’intera finale, mano dopo mano, subisce delle variazioni, poiché a ogni specifica mano, ciò che è già accaduto si considera ormai come evento certo. La probabilità che di solito viene indicata nelle statistiche NBLstats+ e che riportiamo qui sotto, riflette invece la probabilità come se tutte le mani dovessero ancora essere giocate, basandosi su ciò che potenzialmente potrebbe accadere in relazione alle carte che riceveranno i giocatori.
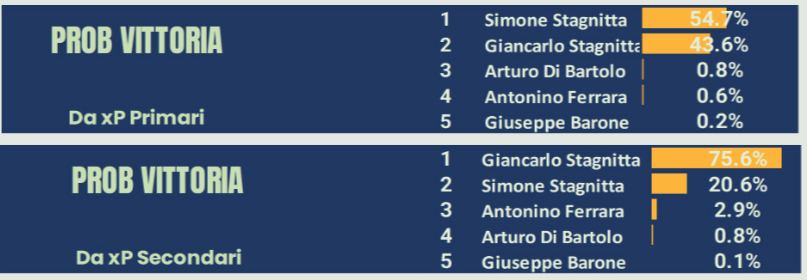
Non viene indicata quindi la variazione di queste probabilità durante lo scorrere delle mani giocate. Se potessimo osservarle mano per mano esse andrebbero a solidificarsi verso un certo valore, in base all’andamento della partita, per avvicinarsi al risultato che effettivamente si concretizzerà. Con l’avanzare delle mani, infatti, la possibilità di cambiare il risultato diventa minore, poiché si riduce la finestra di intervento di un giocatore.
Detto questo, ora vogliamo invece mostrare le probabilità di vittoria della finale al termine della quinta mano; le probabilità riportate sotto in tabella sono diverse da quella sopra riportate, perché considerano come ormai certi i risultati delle prime 4 mani. Inoltre, non indicheremo una sola probabilità per Giancarlo e Simone, ma indicheremo le probabilità di vittoria della partita in base agli scenari che abbiamo scelto:
| Sottoscenario | Probabilità vittoria finale Giancarlo | Probabilità vittoria finale Simone |
|---|---|---|
| Sottoscenario 1: Nessun asso di mazze né 4 di coppe | 54,1% | 45,4% |
| Sottoscenario 2: Gli avversari vincono con briscola o asso di mazze | 95,4% | 3,7% |
| Sottoscenario 3: Controcappotto | 97,9% | 1,2% |
| Scenario 2: Simone prende il giro con briscola | 95,4% | 3,7% |
L’unico sottoscenario/scenario che migliora drasticamente la probabilità di vittoria della finale di Simone è il sottoscenario 1.
Sarebbe semplice suggerire di rischiare, visto che rappresenta l’unica opportunità per ribaltare la situazione. Ma attenzione, è fondamentale non confondere un sottoscenario con una strategia complessiva.
In particolare, ricordiamo che la decisione del giocatore è limitata solamente tra lo scenario 1 e lo scenario 2. La scelta strategica si ferma a questo punto.
Superato tale livello, se si opta per lo scenario 1, il giocatore non ha più alcun controllo sugli sviluppi che esso comporta, in questo caso: il singolo sottoscenario non può più essere considerato una strategia ma solo una parte di una strategia.
Pertanto, è necessario combinare tutti i sottoscenari tramite una media ponderata, trattando lo scenario 1 come unico, unendo, tramite gli opportuni pesi statistici introdotti i diversi sottoscenari.
| Scenario | Probabilità vittoria finale Giancarlo (%) | Probabilità vittoria finale Simone (%) |
|---|---|---|
| Scenario 1 (Media ponderata) | 90.09% | 9.06% |
| Scenario 2 | 95.4% | 3.7% |
A questo punto, possiamo affermare con certezza che lo scenario 1 rappresenta la scelta strategicamente migliore.
La differenza è sensibile ma non determinante, visto che si passa dal 3.7% al 9.06% ma è dimostrato come un tale approccio possa indicare la via strategicamente di maggior guadagno, al netto delle variabili statistiche. L’analisi e le previsioni poi si scontrano con la dura realtà; infatti Simone è andato per lo scenario 1, trovando poi il sottoscenario 3, il quale era tra l’altro il meno probabile tra tutti con il 7.5%.
La briscola, in tutte le sue varianti, è un gioco che va oltre la semplice fortuna o abilità tecnica. È un’arena di decisioni strategiche, dove ogni carta giocata è il frutto di un equilibrio sottile tra rischio e opportunità. L’applicazione dei principi della teoria dei giochi e l’analisi statistica delle partite offrono uno sguardo nuovo su questa disciplina, permettendo di trasformare ogni mossa in una scelta ponderata e consapevole.
Per i giocatori, questo significa abbracciare una mentalità che combina intuizione, calcolo e capacità di adattamento. Non si tratta solo di vincere la mano, ma di giocare con visione, di anticipare, di pensare non solo alla prossima mossa ma a quelle successive.



